逆双曲線関数

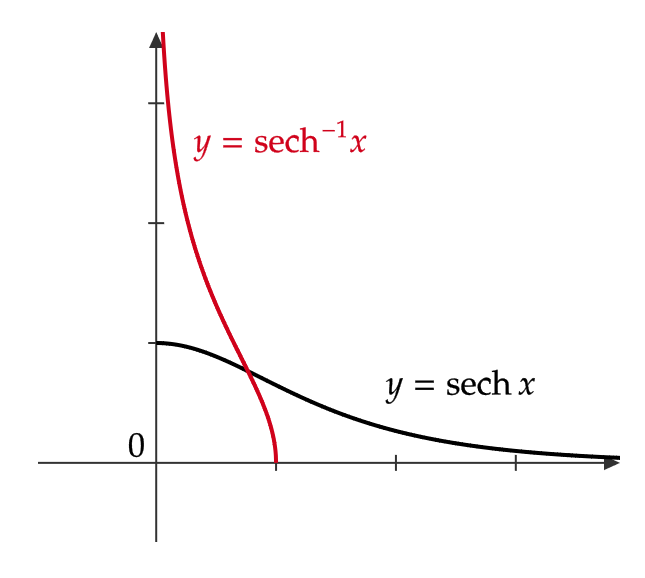
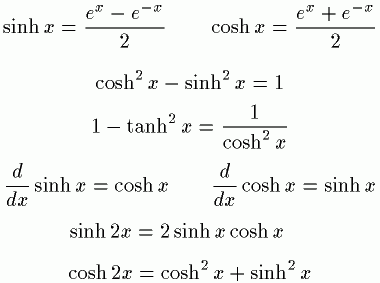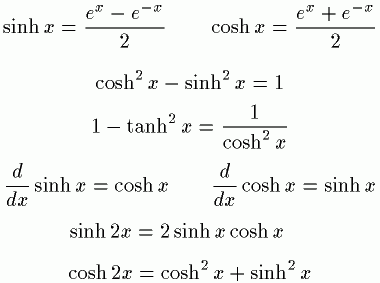逆双曲線関数（ぎゃくそうきょくせんかんすう、英語: inverse hyperbolic functions）は、数学において与えられた双曲線関数の値に対応して双曲角を与える関数。双曲角の大きさは双曲線 x y = 1に対応する双曲的扇形の面積に等しく、単位円の扇形の面積は対応する中心角の2分の1 である。一部の研究者は逆双曲線関数のことを、双曲角を明確に理解するため「面積関数」（英語: area function）と呼ぶ。

逆双曲線関数を表す略記法 arsinh やarcosh とは異なる略記法として、arcsinh やarccosh などが本来誤表記であるにもかかわらず良く使用されるのだが、接頭辞arc はarcus （弓）の省略形であり、接頭辞ar はarea の省略形である。argsinh, argcosh, argtanhなどの表記を好んで用いる研究者もいる。計算機科学の分野では、しばしばasinh という省略形を用いる。累乗を表す上付き文字−1と誤解しないように注意を払う必要があるという事実にもかかわらず、sinh⁻¹(x), cosh⁻¹(x), などの略記も用いられる。また、cosh⁻¹(x)とcosh(x)⁻¹は似て非なるものである。

対数表現

各関数は複素数平面で次のように定義される。

${\displaystyle {\begin{aligned}\operatorname {arsinh} \,z&=\ln(z {\sqrt {z^{2} 1}}\,)\\[2.5ex]\operatorname {arcosh} \,z&=\ln(z {\sqrt {z 1}}{\sqrt {z-1}}\,)\\[1.5ex]\operatorname {artanh} \,z&={\tfrac {1}{2}}\ln \left({\frac {1 z}{1-z}}\right)\\\operatorname {arcoth} \,z&={\tfrac {1}{2}}\ln \left({\frac {z 1}{z-1}}\right)\\\operatorname {arcsch} \,z&=\ln \left({\frac {1}{z}} {\sqrt {{\frac {1}{z^{2}}} 1}}\,\right)\\\operatorname {arsech} \,z&=\ln \left({\frac {1}{z}} {\sqrt {{\frac {1}{z}} 1}}\,{\sqrt {{\frac {1}{z}}-1}}\,\right)\end{aligned}}}$

上記の平方根は正の平方根であり、対数関数は複素対数である。実数の引数、例えばz = xは実数値を返すが、一定の簡素化を行うことが可能であり、例えば ${\displaystyle {\sqrt {x 1}}{\sqrt {x-1}}={\sqrt {x^{2}-1}}}$は正の平方根を使うとき、一般に真ではない。

級数展開

上記の関数は次のように級数展開できる。

${\displaystyle {\begin{aligned}\operatorname {arsinh} \,x&=x-\left({\frac {1}{2}}\right){\frac {x^{3}}{3}} \left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{7}}{7}} \cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{2n 1}}{(2n 1)}},\qquad \left|x\right|<1\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {arcosh} \,x&=\ln 2x-\left(\left({\frac {1}{2}}\right){\frac {x^{-2}}{2}} \left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{-4}}{4}} \left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-6}}{6}} \cdots \right)\\&=\ln 2x-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{-2n}}{(2n)}},\qquad x>1\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {artanh} \,x&=x {\frac {x^{3}}{3}} {\frac {x^{5}}{5}} {\frac {x^{7}}{7}} \cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{2n 1}}{(2n 1)}},\qquad \left|x\right|<1\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {arcsch} \,x=\operatorname {arsinh} {\frac {1}{x}}&=x^{-1}-\left({\frac {1}{2}}\right){\frac {x^{-3}}{3}} \left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{-5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-7}}{7}} \cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{-(2n 1)}}{(2n 1)}},\qquad \left|x\right|>1\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {arsech} \,x=\operatorname {arcosh} {\frac {1}{x}}&=\ln {\frac {2}{x}}-\left(\left({\frac {1}{2}}\right){\frac {x^{2}}{2}} \left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{4}}{4}} \left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{6}}{6}} \cdots \right)\\&=\ln {\frac {2}{x}}-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{2n}}{2n}},\qquad 0$

${\displaystyle {\begin{aligned}\operatorname {arcoth} \,x=\operatorname {artanh} {\frac {1}{x}}&=x^{-1} {\frac {x^{-3}}{3}} {\frac {x^{-5}}{5}} {\frac {x^{-7}}{7}} \cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{-(2n 1)}}{(2n 1)}},\qquad \left|x\right|>1\end{aligned}}}$

またオイラーによるarctanの展開の類似も成り立つ。

${\displaystyle \operatorname {artanh} \,x=\sum _{n=0}^{\infty }{\frac {2^{2n}(n!)^{2}}{(2n 1)!}}{\frac {(-1)^{n}x^{2n 1}}{(1-x^{2})^{n 1}}},\qquad \left|x\right|<{\frac {1}{\sqrt {2}}}}$

${\displaystyle (\operatorname {arsinh} \,x)^{2}=\sum _{n=0}^{\infty }{\frac {2^{2n 1}(n!)^{2}}{(2n 2)!}}(-1)^{n}x^{2n 2},\qquad \left|x\right|<1}$

arsinh x に対する漸近展開は次の式で与えられる。

${\displaystyle \operatorname {arsinh} \,x=\ln 2x \sum \limits _{n=1}^{\infty }{\left({-1}\right)^{n-1}{\frac {\left({2n-1}\right)!!}{2n\left({2n}\right)!!}}}{\frac {1}{x^{2n}}}}$

導関数

${\displaystyle {\begin{aligned}{\frac {d}{dx}}\operatorname {arsinh} \,x&{}={\frac {1}{\sqrt {1 x^{2}}}}\\{\frac {d}{dx}}\operatorname {arcosh} \,x&{}={\frac {1}{\sqrt {x^{2}-1}}}\\{\frac {d}{dx}}\operatorname {artanh} \,x&{}={\frac {1}{1-x^{2}}}\\{\frac {d}{dx}}\operatorname {arcoth} \,x&{}={\frac {1}{1-x^{2}}}\\{\frac {d}{dx}}\operatorname {arsech} \,x&{}={\frac {-1}{x(x 1)\,{\sqrt {\frac {1-x}{1 x}}}}}\\{\frac {d}{dx}}\operatorname {arcsch} \,x&{}={\frac {-1}{x^{2}\,{\sqrt {1 {\frac {1}{x^{2}}}}}}}\\\end{aligned}}}$

実数xに対して、

${\displaystyle {\begin{aligned}{\frac {d}{dx}}\operatorname {arsech} \,x&{}={\frac {\mp 1}{x\,{\sqrt {1-x^{2}}}}};\qquad \Re \{x\}\gtrless 0\\{\frac {d}{dx}}\operatorname {arcsch} \,x&{}={\frac {\mp 1}{x\,{\sqrt {1 x^{2}}}}};\qquad \Re \{x\}\gtrless 0\end{aligned}}}$

微分法の例：θ = arsinh xとおくと、

${\displaystyle {\frac {d\,\operatorname {arsinh} \,x}{dx}}={\frac {d\theta }{d\sinh \theta }}={\frac {1}{\cosh \theta }}={\frac {1}{\sqrt {1 \sinh ^{2}\theta }}}={\frac {1}{\sqrt {1 x^{2}}}}}$

双曲線関数と逆双曲線関数の合成

${\displaystyle {\begin{aligned}\sinh(\operatorname {arcosh} x)&={\sqrt {x^{2}-1}}&{\text{for }}|x|>1\\\sinh(\operatorname {artanh} x)&={\frac {x}{\sqrt {1-x^{2}}}}&{\text{for }}|x|<1\\\cosh(\operatorname {arsinh} x)&={\sqrt {1 x^{2}}}\\\cosh(\operatorname {artanh} x)&={\frac {1}{\sqrt {1-x^{2}}}}&{\text{for }}|x|<1\\\tanh(\operatorname {arsinh} x)&={\frac {x}{\sqrt {1 x^{2}}}}\\\tanh(\operatorname {arcosh} x)&={\frac {\sqrt {x^{2}-1}}{x}}&{\text{for }}|x|>1\end{aligned}}}$

加法公式

${\displaystyle {\begin{aligned}\operatorname {arsinh} u\pm \operatorname {arsinh} v&=\operatorname {arsinh} \left(u{\sqrt {1 v^{2}}}\pm v{\sqrt {1 u^{2}}}\right)\\\operatorname {arcosh} u\pm \operatorname {arcosh} v&=\operatorname {arcosh} \left(uv\pm {\sqrt {\left(u^{2}-1\right)\left(v^{2}-1\right)}}\right)\\\operatorname {artanh} u\pm \operatorname {artanh} v&=\operatorname {artanh} \left({\frac {u\pm v}{1\pm uv}}\right)\\\operatorname {arsinh} u \operatorname {arcosh} v&=\operatorname {arsinh} \left(uv {\sqrt {\left(1 u^{2}\right)\left(v^{2}-1\right)}}\right)\\&=\operatorname {arcosh} \left(v{\sqrt {1 u^{2}}} u{\sqrt {v^{2}-1}}\right)\end{aligned}}}$

逆双曲線関数の恒等式

${\displaystyle {\begin{aligned}\operatorname {arcosh} (2x^{2}-1)&=2\operatorname {arcosh} (x)&{\text{ for }}x\geq 1\\\operatorname {arcosh} (8x^{4}-8x^{2} 1)&=4\operatorname {arcosh} (x)&{\text{ for }}x\geq 1\\\operatorname {arcosh} (2x^{2} 1)&=2\operatorname {arsinh} (x)&{\text{ for }}x\geq 0\\\operatorname {arcosh} (8x^{4} 8x^{2} 1)&=4\operatorname {arsinh} (x)&{\text{ for }}x\geq 0\end{aligned}}}$

関連項目

• グーデルマン関数
• 逆双曲線関数の原始関数の一覧
• 関数一覧

脚注

参考文献

• Herbert Busemann and Paul J. Kelly (1953) Projective Geometry and Projective Metrics, page 207, Academic Press.

外部リンク

• Weisstein, Eric W. "Inverse hyperbolic functions". mathworld.wolfram.com (英語).
• area functions - PlanetMath.（英語）
• Hazewinkel, Michiel, ed. (2001), “Inverse hyperbolic functions”, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Inverse_hyperbolic_functions 
• Hazewinkel, Michiel, ed. (2001), “Area-function”, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Area-function 
• Inverse hyperbolic functions - University College London Department of Mathematics
• 2.22 逆双曲線関数 - 同志社大学・近藤弘一