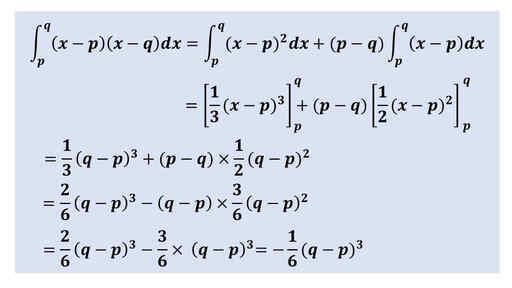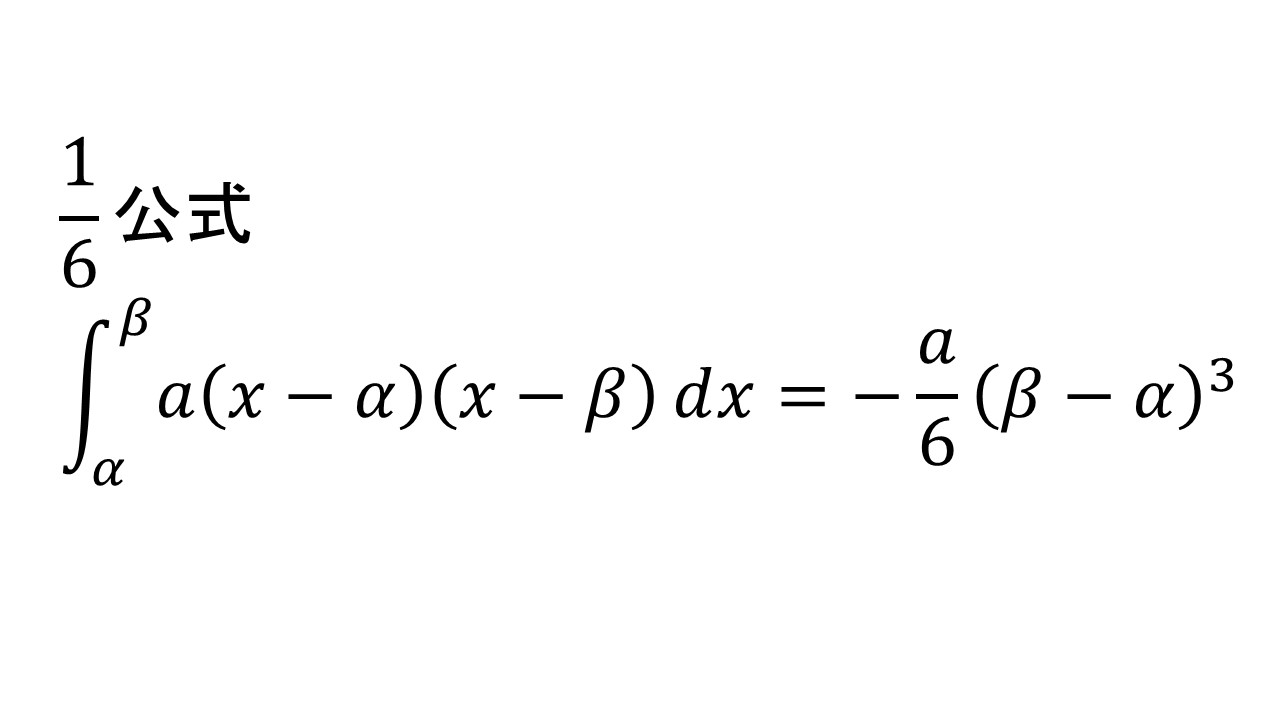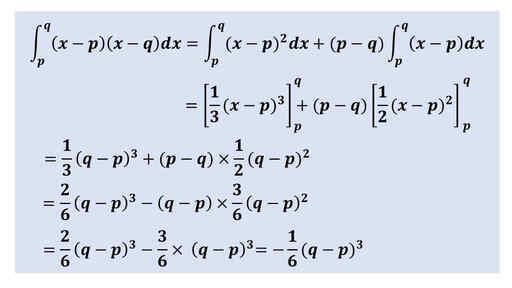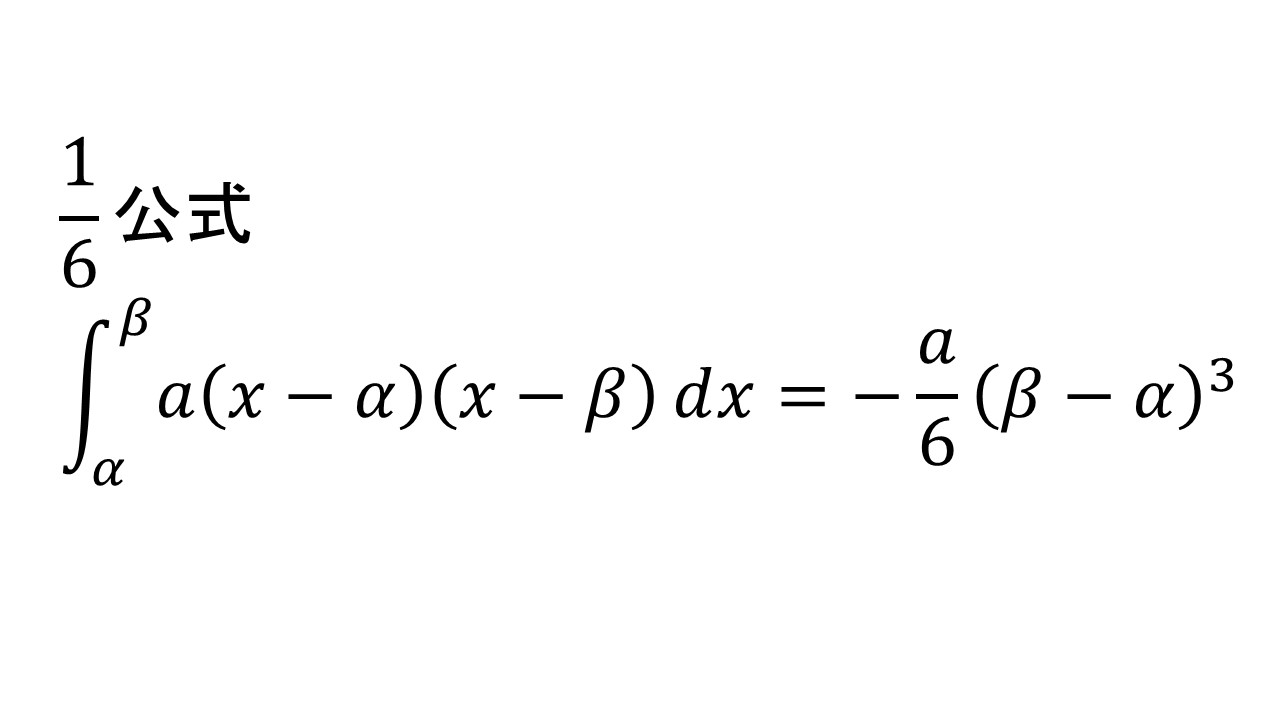1/6公式、6分の1公式（ろくぶんのいちこうしき）は、定積分に関する以下の等式である。

∫ α β ( x − α ) ( x − β ) d x = − 1 6 ( β − α ) 3 {\displaystyle \int _{\alpha }^{\beta }\left(x-\alpha \right)\left(x-\beta \right)dx=-{\dfrac {1}{6}}\left(\beta -\alpha \right)^{3}}

導出

∫ α β ( x − α ) ( x − β ) d x = ∫ α β { x 2 − ( α β ) x α β } d x = [ 1 3 x 3 − 1 2 ( α β ) x 2 α β x ] α β = 1 3 β 3 − 1 2 ( α β ) β 2 α β 2 − 1 3 α 3 1 2 ( α β ) α 2 − α 2 β = 1 3 β 3 − 1 2 α β 2 − 1 2 β 3 α β 2 − 1 3 α 3 1 2 α 3 − 1 2 α 2 β − α 2 β = − 1 6 β 3 1 2 α β 2 − 1 2 α 2 β 1 6 α 3 = − 1 6 ( β 3 − 3 α 2 β 3 α β 2 − α 3 ) = − 1 6 ( β − α ) 3 {\displaystyle {\begin{aligned}\int _{\alpha }^{\beta }\left(x-\alpha \right)\left(x-\beta \right)dx&=\int _{\alpha }^{\beta }\left\{x^{2}-\left(\alpha \beta \right)x \alpha \beta \right\}dx\\&=\left[{\dfrac {1}{3}}x^{3}-{\dfrac {1}{2}}\left(\alpha \beta \right)x^{2} \alpha \beta x\right]_{\alpha }^{\beta }\\&={\dfrac {1}{3}}\beta ^{3}-{\dfrac {1}{2}}\left(\alpha \beta \right)\beta ^{2} \alpha \beta ^{2}-{\dfrac {1}{3}}\alpha ^{3} {\dfrac {1}{2}}\left(\alpha \beta \right)\alpha ^{2}-\alpha ^{2}\beta \\&={\dfrac {1}{3}}\beta ^{3}-{\dfrac {1}{2}}\alpha \beta ^{2}-{\dfrac {1}{2}}\beta ^{3} \alpha \beta ^{2}-{\dfrac {1}{3}}\alpha ^{3} {\dfrac {1}{2}}\alpha ^{3}-{\dfrac {1}{2}}\alpha ^{2}\beta -\alpha ^{2}\beta \\&=-{\dfrac {1}{6}}\beta ^{3} {\dfrac {1}{2}}\alpha \beta ^{2}-{\dfrac {1}{2}}\alpha ^{2}\beta {\dfrac {1}{6}}\alpha ^{3}\\&=-{\dfrac {1}{6}}\left(\beta ^{3}-3\alpha ^{2}\beta 3\alpha \beta ^{2}-\alpha ^{3}\right)\\&=-{\dfrac {1}{6}}\left(\beta -\alpha \right)^{3}\end{aligned}}}

次のように工夫して計算することもできる。

∫ α β ( x − α ) ( x − β ) d x = ∫ α β ( x − α ) { ( x − α ) ( α − β ) } d x = ∫ α β { ( x − α ) 2 ( α − β ) ( x − α ) } d x = [ 1 3 ( x − α ) 3 − 1 2 ( β − α ) ( x − α ) 2 ] α β = 1 3 ( β − α ) 3 − 1 2 ( β − α ) 3 = − 1 6 ( β − α ) 3 {\displaystyle {\begin{aligned}\int _{\alpha }^{\beta }\left(x-\alpha \right)\left(x-\beta \right)dx&=\int _{\alpha }^{\beta }\left(x-\alpha \right)\left\{\left(x-\alpha \right) \left(\alpha -\beta \right)\right\}dx\\&=\int _{\alpha }^{\beta }\left\{\left(x-\alpha \right)^{2} \left(\alpha -\beta \right)\left(x-\alpha \right)\right\}dx\\&=\left[{\dfrac {1}{3}}\left(x-\alpha \right)^{3}-{\dfrac {1}{2}}\left(\beta -\alpha \right)\left(x-\alpha \right)^{2}\right]_{\alpha }^{\beta }\\&={\dfrac {1}{3}}\left(\beta -\alpha \right)^{3}-{\dfrac {1}{2}}\left(\beta -\alpha \right)^{3}\\&=-{\dfrac {1}{6}}\left(\beta -\alpha \right)^{3}\end{aligned}}}

また、部分積分を用いて計算することもできる。

∫ α β ( x − α ) ( x − β ) d x = [ 1 2 ( x − α ) 2 ( x − β ) ] α β − ∫ α β 1 2 ( x − α ) 2 d x = − [ 1 6 ( x − α ) 3 ] α β = − 1 6 ( β − α ) 3 {\displaystyle {\begin{aligned}\int _{\alpha }^{\beta }\left(x-\alpha \right)\left(x-\beta \right)dx&=\left[{\dfrac {1}{2}}\left(x-\alpha \right)^{2}\left(x-\beta \right)\right]_{\alpha }^{\beta }-\int _{\alpha }^{\beta }{\dfrac {1}{2}}\left(x-\alpha \right)^{2}dx\\&=-\left[{\dfrac {1}{6}}\left(x-\alpha \right)^{3}\right]_{\alpha }^{\beta }\\&=-{\dfrac {1}{6}}\left(\beta -\alpha \right)^{3}\end{aligned}}}

利用

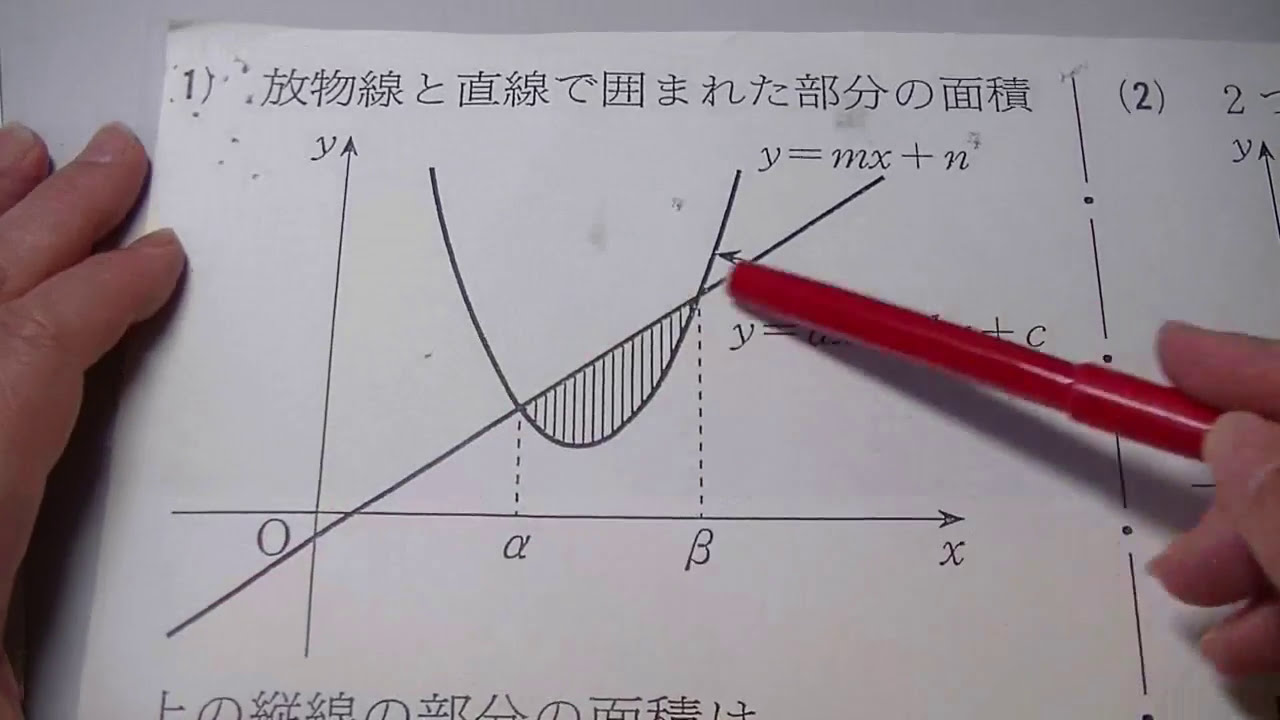
放物線と直線で囲まれた図形の面積を素早く求めることができる。

例えば、xy平面上の放物線 y = x 2 4 x − 5 {\displaystyle y=x^{2} 4x-5} と直線 y = 2 x − 2 {\displaystyle y=2x-2} で囲まれた図形の面積を求めるためには ∫ − 3 1 ( − x 2 − 2 x 3 ) d x {\displaystyle \int _{-3}^{1}\left(-x^{2}-2x 3\right)dx} の計算が必要になるが、これを ∫ − 3 1 − ( x 3 ) ( x − 1 ) d x {\displaystyle \int _{-3}^{1}-\left(x 3\right)\left(x-1\right)dx} と変形すると1/6公式により 1 6 ( 1 3 ) 3 = 32 3 {\displaystyle {\dfrac {1}{6}}\left(1 3\right)^{3}={\dfrac {32}{3}}} となり、素早く計算することができる。

また、1/6公式の応用として、

  • 放物線 y = a x 2 b x c {\displaystyle y=ax^{2} bx c} と直線の交点のx座標を α , β ( α < β ) {\displaystyle \alpha ,\beta (\alpha <\beta )} とおくと、この放物線と直線で囲まれた部分の面積は | a | 6 ( β − α ) 3 {\displaystyle {\dfrac {\left|a\right|}{6}}\left(\beta -\alpha \right)^{3}} と計算できる。
  • 放物線 y = a 1 x 2 b 1 x c 1 {\displaystyle y=a_{1}x^{2} b_{1}x c_{1}} と y = a 2 x 2 b 2 x c 2 {\displaystyle y=a_{2}x^{2} b_{2}x c_{2}} の交点のx座標を α , β ( α < β ) {\displaystyle \alpha ,\beta (\alpha <\beta )} とおくと、この2つの放物線で囲まれた部分の面積は | a 1 − a 2 | 6 ( β − α ) 3 {\displaystyle {\dfrac {\left|a_{1}-a_{2}\right|}{6}}\left(\beta -\alpha \right)^{3}} と計算できる。

1/6公式の一般化として、 ∫ α β ( x − α ) m ( β − x ) n d x = m ! n ! ( m n 1 ) ! ( β − α ) m n 1 {\displaystyle \int _{\alpha }^{\beta }\left(x-\alpha \right)^{m}\left(\beta -x\right)^{n}dx={\dfrac {m!n!}{\left(m n 1\right)!}}\left(\beta -\alpha \right)^{m n 1}} がある。

その他

途中計算の記述が不要であるマークシート試験において、積分計算に使われることがある。

大阪大学の2022年度の文系の数学の入試問題において、1/6公式に似た等式を証明する問題が出題された。

出典


【1/6公式、1/12公式、1/3公式】面積求める公式 全パターン YouTube

6分の1公式、12分の1公式、3分の1公式（大分上野丘高校の生徒からの質問） YouTube

小学16年级数学公式大全（可打印） 知乎

1/6公式 そのマイナスは、どういうことなのか【接点と方程式の重解も解説】 岩井の数学ブログ

1/6公式利用（2次関数と直線で囲まれた面積、2次関数と2次関数で囲まれた面積） 大学受験の王道